ブラウン運動のシミュレーション

離散化された1次元のランダムウォークを体験する。
【キーワード】
ブラウン運動*、熱運動*、拡散現象*
【目的】
ブラウン粒子を駆動させる分子の熱運動の存在や、流体中の拡散現象との関係を通じて、ブラウン運動の起源を理解させる。
【用意するもの】
| 材料 | 個数 | 備考 |
| 方眼紙 | 1枚 | 方眼紙を用意できないときは、普通のレポート用紙でも可。 |
| コイン | 1個 | 確率50%の結果が出るものであれば可。例えば、サイコロ、六角の鉛筆など。学生自身の持ち物を使用させる。 |
【実験時間】
授業中に百回試行するとして、10分程度。
【実験手順】
以下の手順を、学生に実施させる。
- 方眼紙に図1で示したような座標を書き込む。
- コインを投げ上げる。原点(0,0)からスタートし、コインが表の場合には、右に一単位だけ進む((1,1)に移動する)。コインが裏の場合には、左に一単位だけ進む((-1,1)に移動する)。
- 試行ごとに位置を記録しながら、これを100回繰り返す。
- 試行50回目と100回目のときの位置を書き出しておく。また、試行の確率が50%であることを確認するため、表と裏が出た回数も記録しておく。試行の回数が増えるにつれ、50%に近づくことが確認できる。
【教員による説明】
- 実験前に、「50%の確率で左右に移動すると、試行回数が進むにつれて位置が原点の周囲に留まるか、それとも次第に離れるか」と質問する。左右に移動する確率が50%であることに惹かれ、学生は「原点の周囲に留まる」と判断することが多い。
- 実験後、受講者全員の結果を集計する。各人の結果を元に、実際には位置が中央部から離れる者もいることを示す(図1)。また、各人で結果が異なることを述べる。
- 集計した結果を元に、統計的な全体像について説明する(図2)。すなわち、以下のことを説明する。試行50回目と100回目の位置、および、その位置にいた人数を比較する。最初は全員が原点に集中していたが、試行を重ねるにつれて(時間の経過につれて)、中央部にいる人数が減少し、裾野が広がっていく傾向がある。人数が多いほど、滑らかなガウス分布に近づく。
- 図2の理論式を紹介する。時刻ゼロで中央に溶質を置き、
秒後に中央からの地点
の濃度
を拡散方程式から求める。1次元の場合、時間を
、拡散係数を
、とすると、原点からの距離
における濃度
は次式で書くことができる。
この式から、時間が進むにつれ、粒子は拡散して広がることがわかる。
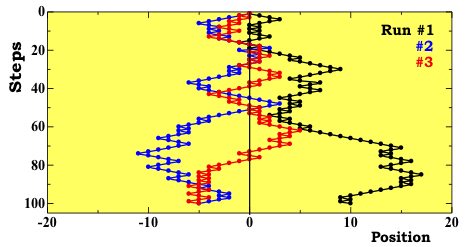
図1.原点(0, 0)からスタートし、50%の確率で左右に一単位づつ進んだ酔歩の例。3人が試行した結果を示す。
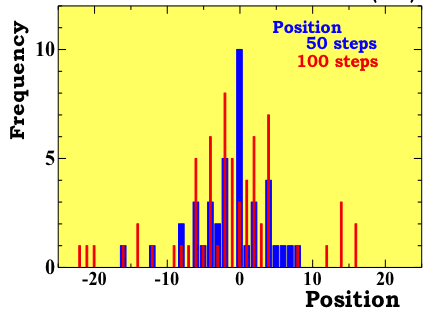
図2.試行50回目と100回目のときの位置、および、その位置にいた人数。50回目の位置は33人、100回目は56人の結果を集計した。
【注意点・備考】
この実験の説明中に、ある学生から、「実際の拡散は、濃度勾配によって広がるのではないか」、つまり、「左右へ移動する確率が異なるのではないか」という指摘が出たことがあった。このような指摘に対しては、「溶質分子が希薄で、それが溶媒分子の熱運動で突き動かされる効果のみ考えたモデルに対応する」と説明することができる。
【関連トピックス】
「花粉」、「金属の電気抵抗の温度変化」「気体の圧力変化」など。
【記事作成者】
三浦 裕一(名古屋大学理学研究科)
最終更新日時: 2014年 05月 12日(Monday) 02:22