斜面を用いた慣性モーメントの理解

慣性モーメントの異なる2つの物体を坂道で転がして、速度の違いを観察する。
【キーワード】
剛体の運動(回転運動)、慣性モーメント
【目的】
質量、回転半径、形状の異なる物体を斜面で転がし、その速度を比較して、慣性モーメントの概念を理解させる。
【用意するもの】
| 材料 | 個数 | 備考 |
| 斜面として使う板 |
1枚 |
縦150cm、横50cmあれば十分。移動式の机が講義室にあれば、それを代用できる。A4サイズの大きさは必要。 |
|
ガラス球 |
2個 |
ビー玉で可。直径が異なるもの2種。 |
| 金属玉 | 1個 | ガラス球の1つと直径をそろえたもの。市販の鉄球やベアリング玉などで可。 |
| 球殻状の物体 | 1個 | ピンポン球で可。 |
| 円柱状の物体 | 4個 | 密度が一様な円柱が望ましい。直径が同じで密度が異なるもの2種。密度が同じで、直径が異なるもの2種。乾電池でも可。 |
| パイプ状の物体 | 1個 | 物理実験準備室で借り入れ可(図1参照)。 |
| 糸巻き状の物体 | 1個 | パイプ状の物体と、質量・直径をそろえたもの。物理実験準備室で借り入れ可(図1参照)。 |
| 定規 | 1本 | 15cmあれば十分。物体を同時にスタートさせるために使用。 |

図1.同じ直径、同じ重さの「糸巻き」と「パイプ」
【実験時間】
30分
【実験準備】
物体を同時にスタートさせられるよう、事前に練習をしておく(【注意点・備考】も参照)。
【実験手順】
(概要):用意した物体を2つずつ斜面で転がす。その際、どちらの物体が速く転がるかを学生に予想させる(予想の理由も聞く)。考察を通じて、物体の転がる速度が、物体のどのような性質に依存し、また依存しないのかを、定性的に理解させる。次に、運動方程式を解くことで、物体の転がる速度が慣性モーメントにどのように依存するのかを、定量的に理解させる。また、慣性モーメントが物体のどのような性質に依存するのかを、定量的に理解させる。最後に、それまでの実験結果と理論的な知識を用いて論理的に実験結果を予想させ、学生の理解を確認する。
- 同じ直径のガラス球と金属球を転がして、その速度を比較する。(結果):同じ速度で転がる。これより、密度が一様な球の転がる速度は質量に依らないことを考察させる。
- 同じ直径の円柱を転がして、その速度を比較する。(結果):同じ速度で転がる。これより、密度が一様な円柱の転がる速度は質量に依らないことを考察させる。1.の結果と合わせて、物体の形状によらず、密度が一様な物体の転がる速度は質量に依らないことを考察させる。
- 異なる直径の2つのガラス球を転がして、その速度を比較する。(結果):同じ速度で転がる。これより、球の転がる速度は直径に依らないことを考察させる。
- 異なる直径の2つの円柱を転がして、その速度を比較する。(結果):同じ速度で転がる。これより、円柱の転がる速度は直径に依らないことを考察させる。3.と合わせて、物体の形状によらず、密度が一様な物体の転がる速度は直径に依らないことを考察させる。
- 球状、球殻状、円柱状、パイプ状の物体をそれぞれ2つずつ転がして、それぞれの速度を比較する。(結果):それぞれの物体の転がる速度の関係は、球の速度>円柱の速度>球殻の速度>パイプの速度、となる。この結果を元に、速く転がる物体が持つ性質を考察させる。
- 【教員による説明】(後述)を行う。また、理論と実験が整合していることを確認する。
- 同じ直径・重さのパイプと糸巻きを転がして、その速度を比較する。(結果):糸巻きの方が速く転がる。これまでの実験、および教員による説明を理解していれば、正しい予想ができるはずである。
【教員による説明】
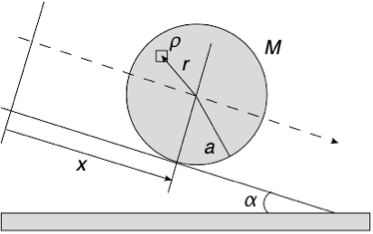 図2.斜面を転がる物体の図 |
剛体が斜面を転がるときの加速度を計算する(図2)。 $$\ddot{x} = \frac{g \sin \alpha}{1+(I/Ma^2)} \qquad (1)$$ $$I = \int \rho r^2 dV \qquad (2)$$ 式(2)から、それぞれの物体について慣性モーメントを具体的に計算すると、$I$が$Ma^2$に依存することがわかる(表1)。よって、式(1)から、表で挙げた形状の物体については、斜面を転がるときの加速度は、その物体の質量と半径には依存しない。$I$の$Ma^2$の係数は物体によって異なり、その係数の大きさの序列が、物体の転がる速度の序列に関係している。係数の大きさは、物体の質量分布で決まる。定性的には、回転軸の外側に質量が分布しているほど、慣性モーメントは大きくなる。 |
|||||||||
|
【注意点・備考】
- 乾電池は密度が一様な円柱ではないが、A4サイズ程度の斜面では、物体の転がる速度の差は充分無視できる。しかし、ある程度長い斜面では、乾電池の密度が一様でない効果が見えてくる。授業において、学生から「物体が転がる速度の差が見えにくいので斜面を長くしたい」という、もっともな提案があったことがある。そのため、できる限り長い斜面と一様な金属円柱(真鍮など)を用いることが望ましい。
- 物体を同時にスタートさせるには練習が必要である。この実験では、15cmの定規で2つの物体を斜面上に止めてから、スタートさせる方法を採用した。この方法では、定規を上方向や横方向に移動させてスタートさせると、物体をわずかに弾いてしまうことがある。そのため、定規を物体の進行方向、つまり斜面下方向に向けて素早く移動させてスタートさせるようにする。実は、この方法は学生から出された提案である。この実験では「学生が自ら工夫して提案する姿勢」を養う効果もあると感じた。
- 表1の慣性モーメントの計算は、学生のレポート問題として課すこともできる。
【動画】
【参考文献】
[1] 島野公利、小出雅之、宮地祐司「ころりん」仮説社、2003年。
[2] 鈴村順三、大島隆義、大澤幸治「理工学の基礎―力学―」培風館、2005年。
【関連トピック】
「回転ドアと慣性モーメント」
重い回転ドアを回転させるには苦労するが、ドアがいったん回りだすと、なかなか止まらない。この性質が死亡事故につながることもある。この「回しにくさ・止めにくさ」を決めているのは「慣性モーメント」である。ドアが同じ重さだとしても、回転する直径が大きいほど、慣性モーメントは大きくなる。
実際に死亡事故が起きた回転ドアでは、以前から大人の骨折事故が何件も起きていたにもかかわらず、悲劇を防げなかった。きちんと対策すれば充分に防げた事故だったのに、国は安全規格を定めていなかった。再現実験から、子どもの頭が挟まれた瞬間、870 kgWの力を受けるという結果が得られた。実際に頭蓋骨が耐えられる力は、大人が200 kgW、子供が100 kgWとのことである。その後、事故を教訓としてJIS規格が作られた。