Rolling Down a Slope

Objects with different moments of inertia roll down a slope at different speeds.
Keywords
Motion of a rigid body (rotational motion), moment of inertia
Objective
We help the students to understand the concepts related to the moment of inertia by comparing the speeds of objects of varying masses, diameters, and shapes rolling down a slope.
Things to Prepare
| Materials | Qty | Remarks |
| A flat surface to be used as a slope | 1 | The slope should have a minimum length of 150cm and a minimum width of 50 cm. It should be larger than A4 in size. A portable desk, if available, in your lecture hall, can be used as a slope, too. |
| Glass sphere | 2 | Marbles will work. Prepare two with different diameters. |
| Metal sphere | 1 | A widely available ball bearing or a steel ball will work. Its diameter must be the same as the diameter of one of the glass spheres. |
| Spherical shell | 1 | A ping pong ball will work. |
| Cylinder | 4 | Prepare two cylinders with different diameters but with the same density. Prepare two cylinders with different densities but with the same diameter. Batteries will work (See Cautionary Note below). |
| Pipe (hallow cylinder) | 1 | Find something like a pipe from Physics Experiment Preparation Room at your school (refer to Fig. 1). |
| Spool | 1 | It should be similar in mass and diameter to the hallow cylinder. . Find something appropriate from Physics Experiment Preparation Room at your school (refer to Fig. 1). |
| Ruler | 1 | The length of about 15cm should be sufficient. It will be used to align the objects at the start line so that they start rolling at the same time. |

Fig. 1. A spool and a pipe having the same mass and diameter.
Experiment Time
30 minutes
Experiment Preparation
Practice several times to make sure that the objects start rolling at the same time (Refer to the [Cautionary Note and Remarks]).
Experiment Procedure
(Abstract): Select a set of two objects and compare their speeds as they roll down the slope. Select another set of two, and keep comparing their rolling speeds…. However, before the experiment, an instructor must encourage students to predict which object will roll down faster in each case. They will present their predictions and hypotheses in class. After the experiment, students will discuss the results in groups and should qualitatively understand which property of a rolling object determines its speed. Then, by solving the equation of motion, the students will quantitatively understand how the rolling speed of an object depends on its moment of inertia. In addition, the instructor must make sure that the students understand which properties of an object determine its moment of inertia quantitatively. Finally, the instructor should test the students’ understandings by asking them to predict the rolling speeds of randomly chosen objects, based on this experiment.
- Roll the glass ball and the metal ball with the same diameter and compare their speeds. (Result): They roll at the same speed. From this result, the students should conclude that the rolling speed of balls with the same diameter is the same, as long as their densities are uniform, and does not depend on their masses.
- Roll two kinds of cylinders with the same diameter and compare their speeds. (Result): They roll at the same speed. From this result, let the students analyze the relation between the rolling speeds and the masses of uniform cylinders with the same diameter. Together with the previous result 1., the students will come to understand that the rolling speeds of objects of uniform density do not depend on their masses, as long as their shapes are the same.
- Roll two glass spheres with different diameters and compare their speeds. (Result): They roll at the same speed. From this result, the students will understand that the rolling speeds of glass spheres do not depend on their diameters.
- Roll two cylinders with different diameters and compare their speeds. (Result): They roll at the same speed. From this result, the students should realize that the rolling speeds of cylinders do not depend on their diameters. Together with the previous result 3., the students will understand that irrespective of their shapes, the rolling speeds of uniform objects do not depend on their diameters.
- Pick two of the following objects: a ball (sphere), a spherical shell, a cylinder, and a pipe or pipe-shaped object, and roll them and compare their speeds. (Result): The students will find that the ball’s speed > the cylinder’s speed > the spherical shell’s speed > the pipe’s speed. Based on these results, let them analyze the properties of the fastest rolling object.
- Explain the physics behind this experiment as show in [Explanation by the instructor] (see below). Make sure that the theory is consistent with the experiment.
- Roll a pipe and a spool of the same diameter and weight, and compare their speeds. (Result): The spool rolls faster. The students should be able to predict this result if they understand the physics behind this experiment explained by the instructor so far.
Explanation by the instructor
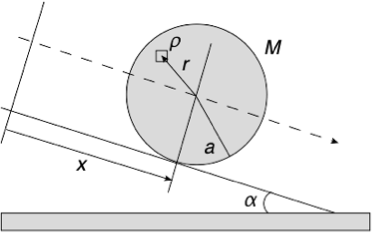
Fig. 2. A diagram of an object rolling down a slope, where $M$ is the mass, $a$ is the radius, and $ρ$ is the density of the objects, and $α$ is the inclination angle of the slope.
Calculate the acceleration when a rigid body rolls down a slope (Fig. 2).
$$\ddot{x} = \frac{g \sin \alpha}{1+(I/Ma^2)} \qquad (1)$$
$$I = \int \rho r^2 dV \qquad (2)$$
When the moment of inertia of an object, $I$, is calculated using equation (2), we can see that $I$ is dependent on $Ma^2$ (Table 1). Therefore, from equation (1), the acceleration of an object given in Table 1, when it rolls down a slope, is not dependent on the mass and radius of the object. The coefficient in front of $Ma^2$ in $I$ varies depending on the shape of an object, and the order of magnitude of this coefficient is related to the order of the rolling speed of the object. This coefficient is determined by the mass distribution of the object. Qualitatively, the more mass distributed outside the axis of rotation, the bigger the moment of inertia.
Table 1. The moments of inertia of objects with various shapes.
| Shape | Moment of inertia $I$ |
| Sphere | $(2/5)Ma^2$ |
| Spherical shell | $(2/3)Ma^2$ |
| Cylinder | $(1/2)Ma^2$ |
| Pipe | $Ma^2$ |
Cautionary Note and Remarks
- A battery does not have a uniform density, however the difference in the rolling speeds of batteries due to their non-uniform densities is negligible enough on a slope of about the size of an A4 sheet of paper. However, on a rather long slope, the effect of non-uniform density will be noticeable. In class, there was a reasonable proposal coming from a student to “increase the length of the slope since it is difficult to notice the difference in the rolling speeds of various objects.” Thus, it is desirable to use a longer slope, if possible, and a uniform metallic cylinder (such as brass and the like) instead of batteries.
- It is very important to practice so that the objects start rolling at the same time. In this experiment, we held the objects on the slope with a 15cm ruler and let them roll at the same time by removing the ruler. However, in this method, the objects sometimes flip slightly before rolling, as the ruler is lifted upward or removed in the transverse direction. To prevent the objects from flipping, one should move the ruler quickly to the forward direction of the objects’ motion, that is, downhill, and allow the objects to roll. This method was suggested by a student. This is an example of our physics demonstration triggering a student’s willingness to propose a plan to devise a method to improve our experiment.
- The calculation of the moments of inertia in Table 1 can also be assigned to the students as homework problems.
Video
References
[1] K. Shimano, M. Koide and Y. Miyaji, Kororin, (Tokyo: Kaetsusha, 2003)
[2] J. Suzumura, T. Oshima and K. Osawa, Rikogaku no Kiso: Rikigaku (Tokyo: Baifukan, 2005)
Related Topics
``Revolving doors and the moment of inertia''
It is difficult to rotate a heavy revolving door; however, once such a door is rotating, it does not stop doing so easily. This property may lead to fatal accidents. The moment of inertia determines “the difficulty to rotate” and “the difficulty to stop” of the revolving door. Among the doors of the same weight, the bigger the diameter of the rotation, the larger the moment of inertia. In reality, many fatal accidents have occurred in revolving doors as well as a large number of bone fracture accidents. These accidents could have been prevented with proper measures, but our country has not even established safety standards for revolving doors. Simulation results show that in a fatal accident when a child’s head was crushed by a revolving door, it must have received a force of 870 kgW. The amount of force that an actual skull can withstand is 200 kgW for adults and 100 kgW for children. Hence, JIS standards were established as a lesson from this accident.
Author of the article
Y. Miura (Graduate School of Science at Nagoya University)